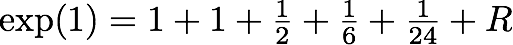Taylor Series¶
Learning about Taylor series can be quite painful. When you first see it, you don’t really know what’s going on, then you’ll be frustrated by having do potentially tricky exercises with computations of the convergence radius or such series and in the end you’ll end up wondering what the heck these series are for. And that’s just Analysis I. Once you start working with several variables, you may meet Taylor series again in a form that either looks exactly like the one dimensional formula just with every index being a ‘multi-index’ now which means there is a lot of implicit cleverness hiding beneath the surface or in a form that’s more explicit and useful but a downright notational nightmare as well.
Only later on, you start appreciating Taylor series. Possibly in complex analysis where they gain a lot of power and simplify things a lot or, for the more practically minded, because Taylor’s theorem gives you a way to approximate things and get a bound for the error. Physicists are particularly notorious for saying things like using the first two terms of the Taylor series will give a precise result
. Which is totally in-character, as the statement is usually blatantly wrong, but still true for all practical purposes.
The most famous Taylor series will be that of the exponential function, developed at 0. Use it for the value 1 and you can approximate Euler’s number. It’s surprisingly easy to do and converges surprisingly quickly.
I.e. the first five terms already give 2,5+ 0,16̅ + 0,0416̅ = 2,7083̅ with the remaining error being smaller than 1/120. Not too shabby.
To perhaps make students think about this and its relevance a bit more, I thought I should point out that if their calculators or computers need to compute trigonometric functions, Taylor series expansions are a way they can achieve that magic. And then I started wondering whether in practice they actually do so. Now that was a bit tricky to find out.
XCode’s help didn’t mention how sin and cos are implemented on the Mac. The best I could find there was a note on Mac OS X PowerPC numerics. The document contains choice passages like this one:
The cosine, sine, and tangent functions use an argument reduction based on the remainder function (see page 5-11) and the constant pi, where pi is the nearest approximation of π with 53 bits of precision. The cosine, sine, and tangent functions are periodic with respect to the constant pi, so their periods are different from their mathematical counterparts and diverge from their counterparts when their arguments become very large.
And that strongly suggests that no Taylor series are used there. In fact, the whole thing is based on a constant π. Which of course is wrong because computer architectures aren’t good at storing irrational numbers. Eeek! Another document on the web (link, as well as many of the others, kindly provided by Tom) suggests that the problem isn’t really PPC specific and that people found Java’s performance ‘bad’ on ‘x87’ because the virtual machine tries to avoid that problem. Amusing quote from that text:
So Java is accurate, but slower. I’ve never been a fan of “fast, but wrong” when “wrong” is roughly random(). Benchmarks rarely test accuracy. “double sin(double theta) { return 0; }” would be a great benchmark-compatible implementation of sin(). For large values of theta, 0 would be arguably more accurate since the absolute error is never greater than 1. fsin/fcos can have absolute errors as large as 2 (correct answer=1; returned result=-1).
While Java might do better because of moving all arguments for these functions in the [0, 2π[ range, this suggests it still doesn’t necessarily use Taylor series. The next question would be whether or not Taylor series expansions actually make sense performance-wise for computers or whether programmers came up with more efficient algorithms for their limited usage cases.
All this still doesn’t make a load of sense to me. Most likely because I’m not a programmer and because strategies for implementing such a non-trivial computations can vary wildly with the times, fashion, hardware they run on and the program they run in. Now I’ve become curious and I’d like to know how various processors and maths libraries compute their trigonometry. So what about making a little table with results for sin(1), sin(100000) and sin(100000000) run on different systems? In fact, we started making one already which will appear in the next post. Be sure to join in and provide more examples – particularly if you have exotic hardware.
Bonus material
- Comments in the dosincos.c code of glibc suggests it uses Taylor series in some implementation. Seems to be some strange vector code(?) So some machines may actually used the beloved and correct series?
- Odd but fast implementation
- Avoiding sines when drawing circles for better performance in retro computing
- Intel maths libraries
- A paper in trigonometry implemention on AMD (€€€)