No Spin¶
943 words on Uni
Started the day with going to the post office posting a couple of things for friends. It was a wholly new discovery of slowliness. I actually had to convince the guy at the counter that the postage rate I wanted to have for my vastly oversized letter did exist (as their web site had told me).
At the next counter there was a really old lady who was walked there by some kind of caretaker. She really was in a bad shape and sat down while he queued for her. When it was their turn it turned out that she wanted to withdraw some money, but her card had expired (and she hadn't gotten the new one), as had her ID. Thus the lady had to apply for a new card and ID, didn't get any money and will have to return in a few days to actually get done what she came for. Not very nice.
Afterwards there was the physics lecture I go to. There was a lot of physics in it today – as opposed to mainly maths – hence it was quite scary and I didn't understand too much. I'll have to bug Gandalf again for further explanations. Then we had our meeting for the lecture I tutor classes for. It was a waste of time, dealing mainly with administrativa which shouldn't be our business anyway. That in turn is mainly the fault of the utterly useless website that's used to 'help' organising the lecture. Sorting out everything manually and typing it up properly afterwards would only have cost a fraction of the time.
In the afternoon, our seminar where a talk was continued from last week. Later on a talk in a series on 4 dimensional space.
The latter was on SO(4) (the group of orientation preserving isometries of four dimensional Euclidian space), and I had hoped to get a nice presentation of its representations and perhaps even Spin(4). But the lecture was very basic, definitely aimed at a very broad audience. And broad the audience was – and equally strange. I expected to see many young students there enjoying the relatively stress-free way of getting to know something. However, there were mainly very old people – old professors partly and some other people I didn't know. Odd.
'4-dimensional space' probably sounds exciting to the non-mathematician. It isn't. As we say: "Just image n-dimensional space and let n=4." I have the impression that in the 'general public' mentioning '4-dimensional' attracts all kinds of weirdos who think it's exciting, somewhat esoteric and of course related to relativity, spacetime and all that jazz. Of course it can be, but it's not the only interest you could have in it. And then again it is exciting:
Many exciting things in geometry and topology happen in dimensions 3 and 4. They tend to be the hardest and cover under the unpretentious name of low dimensional topology. Higher dimensions are often simpler to treat. An example for that is the Poincaré Conjecture. The intuitive explanation for this is that in dimensions 1 and 2 everything is fairly small and there are only so many things you can do. These are studied fairly well and can be dealt with. Then in dimensions 3 or 4 (and sometimes 5) you've got enough space for things to become really tricky and wound up. Once you get to even higher dimensions, things become easier again, as you'll have some extra 'space' to either make sure you can 'avoid' the problems or there is enough space to 'untangle' some twisted setup.
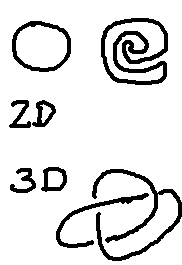A simple example for this may be loops that are embedded into space. Try drawing a closed line, i.e. a line that ends at the same points it starts, without self-intersections on a 2-dimensional sheet of paper. You'll see that however you bend it, what you'll get is essentially a distorted circle. That's quite different in 3-space. With that extra degree of freedom you can actually make a knot, i.e. tangle your line up in a way that it can't be made look like a loop or rubber band without cutting it first. No step up one further dimension and see what happens there. Well, don't 'see', I suppose but imagine. A knot that cannot be untangled in 3-space, can be when it sits in 4-space: The problem when trying to untangle the knot is that you aren't allowed to move the line to pass itself. But with one extra dimension you don't need that anymore – instead of intersecting the other bit of thread, just move it slightly into that extra dimension and there'll be no obstruction left.
Ahem, this was not very precise. So don't beleive it. It was just supposed to give an idea of why having more dimensions may mean you have less problems. You may want to do this more rigorously. Oh my goodness, the web seems to be full of knot theory.
When giving talks, there are many things that can spoil them for the listener, such as: Being badly prepared, being over-prepared with no way to fit everything into the allocated time, being hectic, not talking clearly, not writing clearly, using too many different letters, etc. Usually you can cope with the speaker getting one of them wrong. Not a problem. But several of them can just ruin everything. Oh, and I tend to find listening to people with high-pitch (men and women) voices very strenuous as well.
Oh, and our summer school – the first part of it – seems to be finally taking shape. Fancy some gauge theory?
