Quarter Life Crisis

Now let me try to sketch how mathematicians may prefer to think about this and throw in some fancy words. This will not be entirely rigourous but hopefully illustrates the ideas used.

To begin with, we simplify things. In a first step, we’ll simply omit the painting and just tie the two ends of the rope together – giving a single closed directed loop. As before, we’ll also ignore the fact that there is any back-to-front ordering of the rope and treat the loop as if it is living in a plane with things actually intersecting as they do in the pictures. This could be a real problem – as noted at the end of the previous section – but it turns out that it isn’t, a fact that I don’t want to go into. Thus all we are left with are loops in a plane.

In fact, we are left with loops in a plane with two holes. The holes represent the nails. We can move and deform – but not tear! – the loops freely but we may not move them across holes. That’s pretty much what the nails do in the original picture, if you think about it.

And this is a situation which mathematicians, topologists in particular, love. They’ll burble words like homotopy and fundamental group in this context. Basically we first agree that we want to consider two loops the same if we can continuously, i.e. without tearing, deform one into the other. For example, a loop that is a circle in a plane not containing a hole is considered the same as the loop that is the constant loop at the centre (or anywhere else) of the circle. We can just ‘shrink’ the original loop down in the obvious way.

Convince yourself that the ‘constant’ loop can also be considered a ‘loop’. On the other hand, the first loop we’ve seen just now cannot be deformed into the loop that is a circle which goes around a hole in the plane.

Those classes of ‘essentially the same’ loops are great tools for detecting holes in a plane. It turns out that we can even ‘multiply’ (or ‘add’ if you feel more comfortable with that term – to mathematicians those are mostly the same in this context) those classes of loops under the mild technical conditions that they all start at the same point and something called reparametrisation. I won’t go into details here and also drop the ‘classes of’ in front of ‘loops’ in what follows.

We can introduce the notion of a ‘product’ of two loops starting at the same point. It is the loop we get by running through the first and then through the second loop. We can also take an ‘inverse’ by running through a loop backwards. Taking the ‘product’ with the constant loop we’ve seen above won’t change anything. It’s like multiplying with 1. All this, the classes of loops, the product, constant loop and inverse give what is known as the fundamental group. It’s a good tool for getting to know some basic properties of spaces.

Let me just give three examples. Firstly, the plane without holes: Here, every loop can be deformed to a constant loop. All loops will be considered the same and thus the fundamental group only contains a single element.

Secondly, consider the plane with a single hole. There are two types of loops now. Those enclosing the hole and those that don’t. Again, the latter can all be deformed to a constant loop. But there are more varieties of the former type. Notably, a loop that goes once around the hole clockwise is different form a loop that goes once around the hole counterclockwise or a loop that goes around the hole multiple times in the same direction. It turns out that there are as many different types of loops as there are integers with every loop corresponding to the number of times it goes around the hole counterclockwise (the direction is in fact arbitrarily chosen but mathematicians prefer to think of counterclockwise as the ‘positive’ way to go around something). The ‘product’ from above is just adding of integers and we see that essentially we only need the loop going around the hole once and then we can generate all the other ones by using that loop several times or backwards. The constant loop corresponds to zero.

Thirdly, consider the plane with two holes. This turns out to be much trickier. There are again loops not going around any hole. Then we have a loop going around the left hole once, I’ll call it a, and one going around the right hole once which I’ll call b. For both of these we also have all integer multiples as in the case for a single hole. But what about loops going around both holes? Remember that we could take the product of two loops. And going around both holes will just be the product of b and a: ba. This means that we run around the right hole counterclockwise and then around the left hole counterclockwise in a ‘figure 8’ shape which we don’t run through in the way that the figure is usually drawn, though. As we may deform things a little, we can get rid of the intersection and end up with a loop going around both holes.

Regarding this product, one thing that’s different from computations with numbers, however, is the fact that this is not commutative, i.e. that ab and ba are not the same. Thus, the fundamental group we get for the plane with two holes is the collection of all ‘words’ consisting of the letters a, a^-1, b, b^-1, e.g. ab^-1aaab. Technically this is known as the free product of the integers with themselves, denoted as Z∗Z, where we write Z (from German Zahlen) for the integers.

Now that we’ve got the technicalities sorted, let’s return to our painting. Recall that we have simplified things already to deal with a loop in the plane with two holes. In this simplification recall the solution for the simplified puzzle from above:

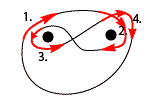
I’ll simplify this up even more now – just by deforming, no cutting happens –, making sure that we have four loops left each of which goes around a single hole only.

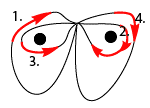
In this setup we can now look at the correspondence between the way we hand our painting and the fundamental group. We have

1. around the left nail clockwise: a^-1,
2. around the right nail clockwise: b^-1,
3. around the left nail counterclockwise: a and
4. around the right nail clockwise: b^-1.

Luckily that’s not too hard. Removing a nail means we ‘fill’ the hole representing it. Looking at that in a slightly different way it means we embed the plane with two holes into the plane with a single hole. Actually we have two such embeddings, one going to the plane with only the left hole and one going to the plane with only the right hole. These embeddings also induce maps between the fundamental groups – a nice property called functoriality – which we can figure out.

After we remove the right hole this means that any loop around the right hole can be deformed to the constant loop. Loops around the left hole will remain the same. Piecing things together, we need to get a map from Z∗Z, the fundamental group of the plane with two holes to Z, the fundamental group of the plane with a single hole. It is given by mapping b to 0 because loops around the right hole can now be deformed to a constant loop and a to 1 as we figured out that stands for a loop that goes around the single hole once. Applying this to our element a^-1b^-1ab^-1 gives (-1)+1 which is zero, corresponding to the fact that the painting falls down.

Removing the left nail will map a to 0 and b to 1 and give us (-1)+(-1) = -2. As before in the concrete case, we can figure out how to ‘fix’ the problem by replacing one of the b^-1s by b.